2024年9月1日実施の中学3年第4回北辰テスト数学。目標偏差値ごとに、解きたい問題、次の目標となる問題などの目安を考えてみました。
それぞれの問題をできるようにするには、どんなことを目標に勉強をすればいいのでしょうか?
偏差値65へのチャレンジ 第3問(2)
第3問は毎回関数の問題が出題されています。(2)は応用問題で、正答率の低い場合が多くあります。
関数の応用問題の正答率はいつも低い傾向がありますが、正答率が同程度の他の問題に比べて解けるようになるが比較的容易な問題であることが多いという特徴があります。
関数は「式を使っていろいろなことを表す」ことが可能な、数学的に頭を使える問題です。数学というのは、複雑なことを簡単に扱うための技術でもありますから、これを適切に練習することで比較的容易に解けるようになります。
今回の問題は偏差値65を目指す人にとってのチャレンジ問題。
第3問(2)のための知識の確認
第3問(2)を解くために必要な知識は次のようなものです。
・一次関数の式
・座標平面での長さの計算
第3問(2)を解きます
問題文を読みながら、図に情報を書き込んでいくと、まずは次のように書き込まれます。
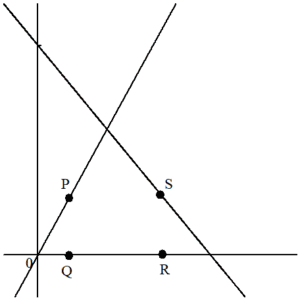
直線lと直線mの式は最初に与えられています。
$${l : y=-x+10}$$
$${m: y=}\frac{3}{2}{x}$$
座標平面上で点は座標が分からなければ使い勝手が悪いですから、点P・点Q・点R・点Sの座標を求めたくなります。
とはいえ、どの点のx座標もy座標もわかっていませんから、点Pのx座標を文字kで置きます。
$${点P ( k ,}\frac{3}{2}{k )}$$
「四角形PQRSが長方形」とありますから、点Qは点Pからx軸に下した垂線の交点です。
$${点Q ( k , 0 )}$$
点Sは点Pとy座標が同じです。x座標は代入して求めることができます。
$${点Sのx座標: }\frac{3}{2}{k=-x+10}$$
これより
$${点Sのx座標: x=-}\frac{3}{2}{k+10}$$
点Sの座標は
$${点S ( -}\frac{3}{2}{k+10 , }\frac{3}{2}{k )}$$
点Rは点Sからx軸に下した垂線の交点ですからx座標は点Sと同じです。
$${点R ( -}\frac{3}{2}{k+10 , 0 )}$$
これで、次のように4つの点の座標がグラフに入りました。
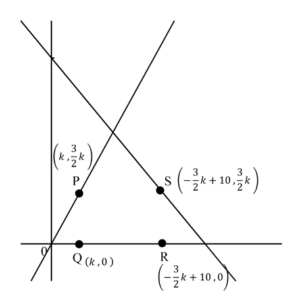
問題文に「QRの長さがPQの長さの2倍」とあります。これを式にしていきます。
$${QRの長さ: -}\frac{3}{2}{k+10-k=-}\frac{5}{2}{k+10}$$
$${PQの長さ:}\frac{3}{2}{k}$$
ですから「QRの長さがPQの長さの2倍」は
$${-}\frac{5}{2}{k+10=2×}\frac{3}{2}{k}$$
これを解くと
$${k=}\frac{20}{11}$$
これが点Pnox座標ですから、点Pの座標はy座標も代入して
$${点P (}\frac{20}{11}{, }\frac{30}{11}{)}$$
と分かりました。
これで解けました。
まとめ
この問題は主に次の2点の考え方で解けます。
1.分からない値は、とりあえず文字で置く (点Pのx座標をkでおいた)
2.問題文の指定したとおりに式にする (QRがPQの2倍)
ほかに特に複雑な式の扱いもなく、問題文の通りに進めれば解けます。
そのため、それほど難しい問題とはいえないでしょう。
ところで、今回は点Pのy座標から点Sの座標を求めましたが、他の進め方もできます。
点Qの座標を求めた後、PQの長さを求めます。
$${PQの長さ:}\frac{3}{2}{k}$$
問題文にある「QRがPQの2倍」から
$${QRの長さ:}\frac{3}{2}{k×2 = 3k}$$
として、点Rの座標を与えます。
$${点R: (4k, 0 )}$$
このx座標と点Pのy座標から点Sを
$${点S: (4k, }\frac{3}{2}{k )}$$
として、この点Sが直線l上にあるために、直線lの式に代入して
$$\frac{3}{2}{k = -4k+10}$$
これを解いて
$${k=}\frac{20}{11}$$
このように求めることもできます。
どちらも、問題文の通りに式を作って座標を与えていきます。そのため、どちらも解くための難易度や面倒くささは同じくらいだと思います。
今は偏差値60くらいだけど、65を超えたい人は、ぜひチャレンジしてみるべき問題でしょう。

