2024年6月実施の中学3年第2回北辰テスト数学。目標偏差値ごとに、解きたい問題、次の目標となる問題などの目安を考えてみました。
それぞれの問題をできるようにするには、どんなことを目標に勉強をすればいいのでしょうか?
偏差値70へのチャレンジ 第3問(2)
第3問は毎回関数の問題が出題されています。(2)は応用問題で、正答率の低い場合が多くあります。
関数の応用問題の正答率はいつも低い傾向がありますが、正答率が同程度の他の問題に比べて解けるようになるが比較的容易な問題であることが多いという特徴があります。
関数は「式を使っていろいろなことを表す」ことが可能な、数学的に頭を使える問題です。数学というのは、複雑なことを簡単に扱うための技術でもありますから、これを適切に練習することで比較的容易に解けるようになります。
今回は偏差値70へのチャレンジ問題。
第3問(2)のための知識の確認
第3問(2)を解くために必要な知識は次のようなものです。
・一次関数の式の求め方
・一次関数の傾きが、グラフでどのように見えるか
・長方形と三角形の面積の求め方
第3問(2)を解きます
問題文を読みながら、図に情報を書き込んでいくと、まずは次のように書き込まれます。
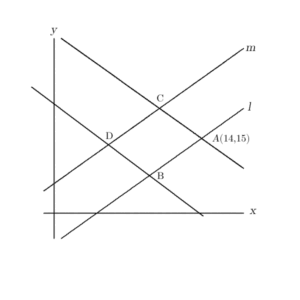
直線lと直線mの式は最初に与えられています。
$${l : y=}\frac{3}{2}{x-6}$$
$${m: y=}\frac{3}{2}{x+6}$$
また(2)の問題文で点Aの座標が(14,15)ということと、直線ACと直線BDの傾きが与えられます。
直線ACについては、傾きと通る点が分かりますので、式を求められますから、求めてしまいましょう。
直線ACの切片をbと文字で置いて
$${直線AC y=-}\frac{3}{2}{x+b}$$
この直線は(14,15)を通るということなので
$${ 15=-}\frac{3}{2}{×14+b}$$
これより
$${b=36}$$
よって
$${直線AC y=-}\frac{3}{2}{x+36}$$
この段階で、直線ACと直線mの交点Cの座標も求められますので、求めてしまいましょう。
$${点C }\frac{3}{2}{x+6=-}\frac{3}{2}{x+36}$$
より
$${x=10}$$
$${y=21}$$
また、この様子をグラフに書き入れてしまいます。
このとき、ACの傾きと合っているか確認できるように直角三角形も書き入れてしまいます。
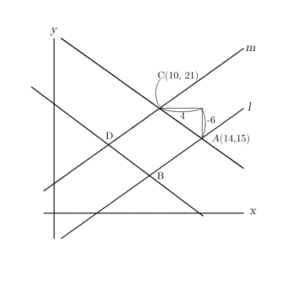
次に、四角形ACDBの面積が76と問題文で指定されます。
ここで、四角形ACDBの面積をどう求めようか考える必要があります。
とはいえ、面積を求めるときの方針は、基本的に次の3つですから、それほど色々と考える必要はありません。
方針1.面積の公式を使って直接求める
方針2.面積が求められる小さい図形に分けて、足し合わせる
方針3.面積が求められる大きな図形から、余分を引く
この問題では、方針1の直接求めるというのはどうでしょうか?
四角形ACDBが平行四辺形ですから「横×高さ」で求められます。けれども、関数のグラフであるxy平面では、x軸やy軸と平行な直線の長さは使い勝手がいいのですが、斜めの直線の長さは使うのが面倒です。少なくとも中3の2学期に学ぶ三平方の定理がなければ、長さを求めることすら困難です。ですから、ここではこの方針はやめておきます。
方針2はどうか?
方針2で小さく分けるとき、与えられている点と点を結んで分けるのは自然ですが、まだグラフ上にない点を新しくつくり、この点と結んで分けるのは、思考を難しいものにしてしまいます。脈絡のない点はできるだけ使わない方が良いでしょう。この問題では、次のような分け方なら比較的自然でしょうか。
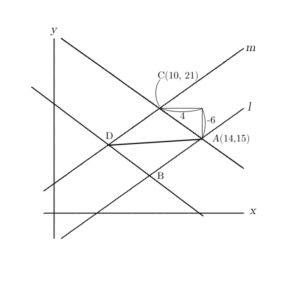
または
どちらの分け方でも、三角形2つに分けられています。どの三角形の辺もx軸やy軸に平行でない、または平行と決まっていない直線なので、やはりメンドウが予想されますから、ここではやめておいた方が無難でしょう。
最後に方針3です。
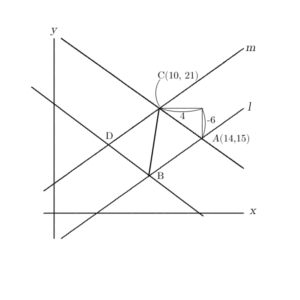
大きい図形から余分を引くというのは、今回のグラフでは次のような感じでしょう。
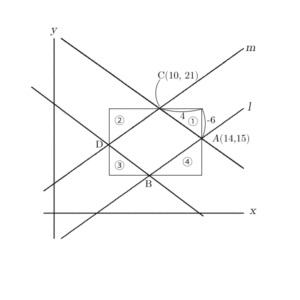
大きな長方形から、①、②、③、④の4つの三角形を引く感じです。
この場合、長方形も、三角形4つもx軸、y軸に平行な直線を使って作られていますし、面積を求めるために使う「横、縦」「底辺、高さ」がx軸やy軸に平行です。このアドバンテージあるので、この方針で進めます。
さて、グラフを見ると、①と③が合同な気がします。確かめてみると、①と③の直角三角形の斜辺ACと斜辺BDは平行四辺形の対辺なので長さは同じです。また、錯角をつかえば、1つの鋭角が等しいことも分かるので、①と③は合同です。
①の面積は底辺と高さがもう分かっていますから、①と③の部分は解決です。
②と④の三角形も同じように合同です。けれども、この2つの三角形も、長方形の面積も求めることはまだできません。特にきっかけもないようですので、横と縦を次のように文字で置いてします。
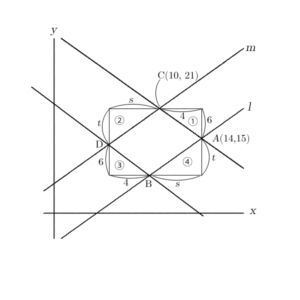
②と④の三角形の横の辺の長さをs,縦の辺をtと文字で置きました。また、①の三角形の縦の辺を傾きの確認のため-6としていましたが、長さとしてみたいので6にしてあります。
ここで、④の三角形でsとtが直線lの傾きを表していることに着目すると、次の式が成り立ちます。
$$\frac{t}{s}{=}\frac{3}{2}$$
この式はまだ使うか分かりませんが、作っておきます。情報はあった方が良いので。
さて、四角形ACDBの面積が76ということを式で表せます。
長方形から4つの三角形を引いたら76です。
$${(s+4)(t+6)-4×6×}\frac{1}{2}{×2-s×t×}\frac{1}{2}{×2=76}$$
何だか複雑な式で、イヤになってきますが、とりあえず整理してみます。転回すると
$${st+4t+6s+24-24-st=76}$$
運がいいことにstの項が消えてくれそうです。
$${st+4t+6s+24-24-st=76}$$
$${4t+6s=76}$$
ここで、さっき書いておいた傾きの式が役に立ちそうです。
$$\frac{t}{s}{=}\frac{3}{2}$$
より
$${t=}\frac{3}{2}{s}$$
これを代入して
$${4×}\frac{3}{2}{s+6s=76}$$
解くと
$${s=}\frac{19}{3}$$
$${t=}\frac{19}{2}$$
となります。これを使って点Aから点Bを求めると
$${点Bのx座標 14-}\frac{19}{3}{=}\frac{23}{3}$$
$${点Bのy座標 15-}\frac{19}{2}{=}\frac{11}{2}$$
$${点B (}\frac{23}{3}{, }\frac{11}{2}{)}$$
問題で求めるのは直線BDの式です。
ここまでで直線BDの傾きと通る点が分かりました。
$${傾き:-}\frac{3}{2}$$
$${通る点B (}\frac{23}{3}{, }\frac{11}{2}{)}$$
から、直線BDの切片を文字cで置いて、代入して求めます。
$${直線BD y=-}\frac{3}{2}{x+c}$$
代入すると
$$\frac{11}{2}{=-}\frac{3}{2}{×}\frac{23}{3}{+c}$$
これを解いて
$${c=17}$$
となりますから、直線BDの式は次のようになります。
$${直線BD y=-}\frac{3}{2}{x+17}$$
これで解けました。
まとめ
この問題でも、色々と試行錯誤する前にできるだけ基本に近いように面積を求めようとすべきでしょう。このとき、グラフではx軸と平行やy軸と平行な直線は使いやすいが、斜めの直線は使いづらいというのは重要です。使いづらいものはできるだけ避けた方がよいのです。わざわざ難しいことをするより、文字や式を使って式を作り、難しい思考は数学の力に任せましょう。こうして数学の使い方を練習した方が、色々と考える練習をするより、おそらくは数学を使えるようになるでしょう。そして数学を使えるようになることで、より複雑なことを扱えるようになります。
この問題で難しいところは次の2つの部分でしょう。
・四角形ACDBの面積を求める方針の選び方
・sとtの文字で置いたとき、傾きの式も作っておく
これらは確かに初めは難しいと思います。だから偏差値70へのチャレンジ問題なのですが、トレーニングすればできるようになるレベルではないかと思います。

