2024年6月実施の中学3年第2回北辰テスト数学。目標偏差値ごとに、解きたい問題、次の目標となる問題などの目安を考えてみました。
それぞれの問題をできるようにするには、どんなことを目標に勉強をすればいいのでしょうか?
偏差値60超えへのチャレンジ 第1問(7)
北辰テストでは、基本的な計算のしかたや、基本的な問題の解き方を一通りできるようにしておけば、偏差値60くらいまではいきます。
偏差値60を超えて65を目指そうとするあたりから、ちょっと勉強の着目点を変える必要が出てきます。
数学でも他の科目でも、何かを表すための言葉が使われます。第1問(7)では「箱ひげ図」とか「中央値」「四分位数」などです。
これらの言葉は、あることを表すための名前として付けられていますから、それぞれが何を表すのかを覚えなければなりません。
「定義を覚える。」とか「定義に着目する」とか言われます。
これらは「解き方」というより「言葉の決まり事」ですから、「どう解くか」の練習の前に「どんなことを表す言葉か」を覚えておかなければなりません。
この定義への着目は、勉強ができる人にとっては”あたりまえ”のように感じることですが、実際は”あたりまえ”と言えることではありません。これを”あたりまえ”のようにすることが、偏差値60を超えるときに、必要になることの1つです。
第1問(7)のための知識の確認
第1問(7)は箱ひげ図の問題です。
箱ひげ図は次のような図です。
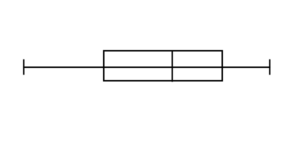
データの分析で学んだ図で、ヒストグラムを次のことを見やすくするように書き直したような感じです。
「最小値」「第一四分位数」「中央値」「第三四分位数」「最大値」
それぞれの言葉が何を表すのかを見てみます。それぞれの定義です。それぞれの言葉が何を表すのか(定義)をまず書きます。その次に、それが具体的にどんなことかを「例えば11個のデータの場合」などの例で書いています。例は、その前に挙げた定義を説明するために書くものですから、定義で分かった人は読む必要はありません。
定義というのは、広く色々な場面で使うことですから、一般的な表現で書かれます。一般的というのは「一部の例外のある可能性はあるけれど多くのものに使える」という感じの意味です。広く色々な場面で使うためには、一般的な言葉で書く必要があるのです。一般的な言葉は抽象的ともいわれたりします。
広く色々なものは、この言葉通り色々なものが含まれるます。そのどれもを含むような表現にしなければなりません。そのために、あいまいな言葉の必要があるのです。
けれども、一般的な言葉は、広く使えますが、あいまいで分かりづらいものです。あいまいで分かりづらいですから「例えば」とかで説明が必要になります。「例えば」のような説明を具体と言います。具体的な説明は、あくまで定義を理解するための説明ですから、具体的な説明の部分だけわかったのでは不十分です。具体的な説明から、定義などの一般的な説明が何を意味しているのかが分かればOKです。
(これは、国語の文章の読み方と一緒です。)
では、それぞれの言葉について。
「最小値」・・・一番小さい値
「中央値」・・・データの真ん中の値。
真ん中の値といっても、バラバラでは真ん中の決めようがありませんから、小さい順または大きい順に並べたときの真ん中の値です。
例えば、データが11個など奇数のときは、データを半分で分けると下位に5つのデータ、上位に5つのデータがあり、下から6番目、上から6番目が真ん中になります。データが10個などの偶数のときは、真ん中にはデータがありませんから、真ん中の両脇のデータの平均を中央値とします。データが10個なら、下から5番目のデータと6番目のデータの平均です。
中央値はこのような定義ですから、「小さい順(大きい順)に並べること」が最初に行うことになります。
「第一四分位数」・・・下位半分のデータの真ん中。全体の下から4分の1の順番です。
例えばデータが10個などのときは、下位半分が5つのデータ、と上位半分が5つのデータになっています。
下位半分の5つのデータは下位2こ、真ん中1こ、上位2こに分けられます。この真ん中は下から3番目です。これが第一四分位数です。
データが12個などのときは、下位半分のデータが6個になります。このときは、下位半分は下位の下位3個と下位の上位3個になりますから、下位半分の真ん中は、その両脇のデータの平均とします。
「第三四分位数」・・・上位半分のデータの真ん中。
第一四分位数と同じように、上位半分に対して行う。
言葉では分かりづらいですね。
図にすると、シンプルに見えます。
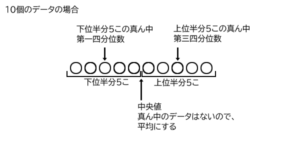
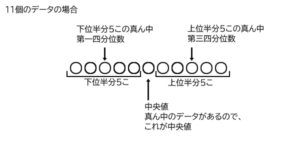
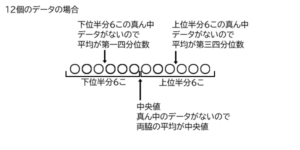
中央値は「中央の値」、第一四分位数は「4つに分けた1番目の値」など、数学や理科では、名前(言葉)が内容を表す場合も少なくありません。名前から内容が推測できるように理解してくと良いと思います。
第1問(7)を解きます
問題は「9人のデータ」の箱ひげ図に関する問題です。
ゲームの得点についての箱ひげ図です。
先に箱ひげ図の読み取りです。
箱ひげ図より
最小値 1
最大値 9
第一四分位数 3
中央値 6
第三四分位数 7
と読み取れます。
次に中央値などをデータから見ていきます。「小さい順(大きい順)に並べる」ことが最初に行うことです。
ですが、今回は問題が並べてくれてあります。
ゲームの得点データは、小さい順で
a,b,4,4,c,7,7,d,9
となっています。
ここから、最小値がa、最大値が9と分かります。
この段階で a=1 が決まります。
半分に分けます。
下位半分 a,b,4,4
真ん中 c
上位半分 7,7,d,9
中央値が c のようですから、ここで c=6 となります。
下位半分の真ん中が第一四分位数です。
下位半分 a,b,4,4 ですが、a=1と分かっていますから、
1, b, 4,4 が正体です。
この真ん中は 、bと4の平均(またはbと4の真ん中)です。
箱ひげ図から第一四分位数は 3 ですから、
bと4の真ん中が3 であることから、 b=2となります。
または、式にして
$$\frac{b+4}{2}{=3}$$
これより b=2 としても良いと思います。
同じように第三四分位数。
上位半分は
7,7,d,9 で、 7とd の真ん中(平均)が第三四分位数です。
箱ひげ図より第三四分位数は7ですから、d=7と分かります。
これも式にして
$$\frac{7+d}{2}{=7}$$
から d=7 と求めても良いと思います。
まとめ
このように「言葉(名前)の定義を覚えること」が増す必要です。
そして、箱ひげ図から読み取ること、そして箱ひげ図から読み取ったことと、データ(小さい順)とを丁寧に結びつけていくこと。
このようにして解かれる問題です。
定義、読み取り、丁寧な扱い
この3つが偏差値60を超えるあたりから必要になります。これらを身につけるには、大量の演習より、着目をしっかり意識した丁寧な演習が重要です。

