2024年4月28日に実施されました、中学3年第1回北辰テスト。
数学には、問題の難易度(特に複雑さ)と正答率のマッチしない問題がいくつかありました。( 2024年4月北辰テスト 数学 難易度と正答率が合っていない問題 )
比較的シンプルな問題でありながら正答率が低い問題が2題ありましたが、どちらも関数の問題です。この2題のうち第3問(2)について復習しました。
正答率の低い関数の問題、本当に難しい?
正答率が低い問題のもう1題は第1問(7)です。
それぞれの正答率は
第1問(7)
全体 13.1%
偏差値70以上 75.6%
偏差値65以上 46%
第3問(2)
全体 6.0%
偏差値70以上 63.9%
偏差値65以上 28.1%
正答率では、第3問(2)の方が低いのですが、解くために使う基礎知識としては、第3問(2)の方が簡単なものです。
使う基礎知識を比較してみます。
第1問(7)で使う基礎知識
・関数の式に代入して点の座標を求める
・変化の割合の定義
第3問(2)で使う基礎知識
・関数の式に代入して点の座標を求める
・x軸に平行なら、y座標の値が同じ
・y軸に平行なら、x座標の値が同じ
・x軸やy軸に平行な直線の2点間の長さを求める
・1次方程式を解く
第3問(2)の方が多いのですが、どれも多くの中学生ができる内容ばかりです。第1問(7)については、変化の割合の定義を使える中学生が多くないのです。
変化の割合は「1次関数ならば公式のように求められるけれど、定義により解いているわけではないので、他の関数では解けない。」という中学生が多いのです。
けれども、第3問(2)については、このようなことはあまり見られません。
そのため、第3問(2)の方が簡単だとも考えられるのですが、正答率がとても低いのです。解けないのではなく、時間がなかったのか、問題文が長いか読まずに飛ばしたのかもしれません。一番多いのは「やってみようとする前に、解けなさそうだから解かなかった」という人かもしれません。このような生徒の意見はよく聞きます。
ところで、どうしてやってみる前に、解けなさそうと分かったのでしょうか?不思議です。
やってみなければ、解けるか解けないかは分からないはずです。問題は「解き方が思い浮かぶ = 解けそう」で、「解き方が思い浮かばない = 解けなさそう」という勉強です。
この原因を色々と探してみるのですが、可能性としては勉強が「解き方を学ぶもの」になっているからと思います。
けれども、勉強は「解き方を学ぶもの」ではありません。
初めはあまり違わないように思う人も多いですが、勉強は「どうなっているか?を知るもの」です。物事や現象の理解のしかたや、どうなっているかを把握するための道具が勉強と考えています。このように勉強を進めると、応用は楽です。(計算練習はしっかりとしなければなりませんが。)
第3問(2)
第3問(2)を解き進めます。
解き方は「問題に従うこと」だけです。
問題に従うというのは
・問題文を読みながら、紹介された点の座標を与えること。ただし、x座標の値やy座標の値が分からないときは、文字で置きます。
・式にできることは、問題文の言葉を式にすること
この2点です。
文字で置くというのは、数学ではよく使います。とりあえず「分からない値は文字で置く」と考えておいても構わないでしょう。
ただ、この問題では問題文の後半で「点Aのx座標をtとする」と指定されます。はじめに後半を確認しておけば、最初からtを使えばいいですが、そうでない場合は適当な文字でおいておいて、後でtに直す感じでも良いと思います。
進めます。
問題文を読んでいくと
点Aがすぐ出てきます。
点Aのx座標をtとして、関数の式に代入して点Aの座標を求めます。
$${点A(t,t+2)}$$
次に点B。点Bは、点Aからy軸に平行に直線を引き、直線mと交わった点ですから、点Aとx座標が同じtです。これを直線mの式に代入して座標を求めます。
$${点A(t,}\frac{1}{2}{t)}$$
同じように点C。点Cはx軸と並行ですから、点Aをy座標が同じです。これを直線mの式に代入して、x座標を求めます。
$${t+2=} \frac{1}{2} {x}$$
$${x=2t+4}$$
$${点C(2t+4,t+2)}$$
次に点D。点Dは点Cを通ってy軸に平行な直線とx軸との交点です。x座標は点Cと同じです。x座標上では、y座標が0です。
$${点D(2t+4,0)}$$
ここまでで、問題文の1段落が終わります。
点は図に書き込みながら目に見えるようにしていく方が楽ですから、次の図のようになっています。
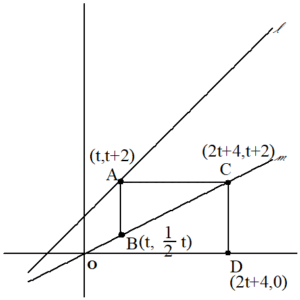
第2段落最初に AB+AC+CD=15 とありますので、これをグラフを見ながら式にしていきます。
$${AB=t+2-}\frac{1}{2}{t}$$
$${AC=2t+4-t}$$
$${CD=t+2}$$
となりますので
AB+AC+CD=15 は次の式になります。
$${t+2-}\frac{1}{2}{t+2t+4-t+t+2=15}$$
これでtの方程式ができましたので、整理して解きます。
$$\frac{5}{2}{t+8=15}$$
$$\frac{5}{2}{t=7}$$
$${t=}\frac{14}{5}$$
こうして、tの値が分かりましたので、点大にゅして研鑽すればAの座標が分かります。
$${点A(}\frac{14}{5}{,}\frac{24}{5}{)}$$
これで終わりです。
途中が少し長いですから、問題文を最後まで読んでから解こうと思うと、混乱してしまって難しいと感じるかもしれません。
「どうなっているか」が分からないのに「どう解こうか?」と考えれば難しいのは道理です。「どうなっているか」を頭の中だけで把握しようとする習慣が、問題を難しく感じさせると言ってもいいのかもしれません。
そうではなくて、問題文を読みながら、その順に従って点を求め、式を作っていくことは「どうなっているか」を把握しながら進めることです。この場合は、最後に「点Aの座標を求めよ」と言われても、もうほとんどが分かっていますから、あとは作ってある方程式を解くだけて答えが出ることが分かるでしょう。
このようなことは、大人や勉強ができる人からすれば当たり前に思えることかもしれませんが、それができないのです。そうなるように学んでいないのです。
そして、当たり前と思える人も、勉強をしながら体系的にこの視点を身に着けられたら、もっと明確になりますから、もっとできるようになるでしょう。
練習すれば、多く人のができる問題でしょう。チャレンジする価値があります。

