2024年6月実施の中学3年第2回北辰テスト数学。目標偏差値ごとに、解きたい問題、次の目標となる問題などの目安を考えてみました。
それぞれの問題をできるようにするには、どんなことを目標に勉強をすればいいのでしょうか?
偏差値80へのチャレンジ 第4問(3)
第4問(3)は北辰テストの最後の問題ですが、ほぼ毎回、難問です。正答率もかなり低いです。
とはいえ、難問でも、本当にムリな問題から、丁寧に進めれば解くのは比較的ムリではない問題まであります。
2024年6月の中3第2回では、丁寧に進めればムリではないレベルでしたので、進め方を軽く触れてみます。
第4問(3)のための知識の確認
第4問(3)を解くために必要な知識は次のようなものです。
・三角形の合同条件
・三角形の面積の求め方
第4問(3)を解きます
(1)で合同を証明していますので、このときまでに分かった情報を図に書き込んでいくと、まずは次のように書き込まれます。
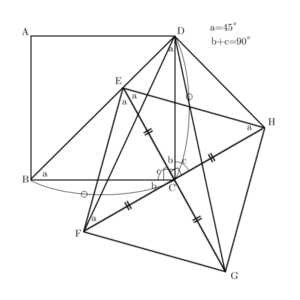
次に(3)の問題文の情報を確認して、適宜式にしていきます。
まず「四角形ABCDの面積が55」とあります。
ABCDは正方形ですので。この一辺の長さをLと置くと
$${L×L=55}$$
次に「△DFGの面積が45」とあります。
△DFGの面積ですから、底辺と高さを決めます。
底辺をFGとするのが楽そうですから、高さは点Dから辺FGに引いた垂線にします。FGを t とします。高さはtを途中まで使えますので、次の図のよう t+h と置きます。
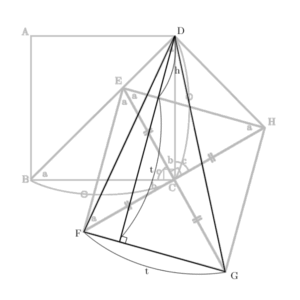
このように置いた文字を使って
$${t×(t+h)×}\frac{1}{2}{=45}$$
と式にしておきます。
最後に「△CHEの面積を求めなさい」となります。△CHEは正方形EFGHの4分の1ですので、ここまでの設定を使うと
$${△CHE=t×t×}\frac{1}{4}$$
これで設定が終わりました。
とはいえ、ここまでで設定した式だけでは解けません。さすがに北辰最後の問題です。
ここからが難しいところです。
何が難しいかといえば「同じ面積の図形を探すこと」です。
同じ面積の図形を探すには次の2つの方法が考えられます、
1.等積変形
2.合同
等積変形はやや複雑なことを考えなければならないので、先に合同な図形を探します。これまでで、色々と同じ大きさの記号が入っていますので、まずこれを頼りに探します。
まず(1)から「△FCI≡△ECJ」
他に
「△DCH≡BCH」(2辺とその間の角)
「△JCH≡△ICE」(2辺とその間の角)
まずはこのくらいでしょうか。
このうち、△DCH≡△BCHに着目します。
というのも、次のように面積を式にできるからです。
まず
$${△DBC=L×L×}\frac{1}{4}$$
つぎに
$${△DBC=△BCH+△DEC}$$
また
$${四角形DECH=△DCH+△DEC}$$
これより
$${四角形DECH=L×L×}\frac{1}{4}$$
ところで四角形DECHは次のようにも計算できます。
$${四角形DECH=△DEH+△ECH}$$
$${=t×h×}\frac{1}{2}{+t×t×}\frac{1}{4}$$
こうして、四角形DECHより次の式を得ます。
$$\frac{1}{2}{th+}\frac{1}{4}{t^2}{=}\frac{1}{2}{L^2}$$
ここで四角形ABCDの面積が55ですから
$${L^2=55}$$
$$\frac{1}{2}{th+}\frac{1}{4}{t^2}{=}\frac{55}{2}{・・・①}$$
一方、△DFGより次の式ができています。
$$\frac{1}{2}{th+}\frac{1}{2}{t^2=45・・・②}$$
また、求める△CHEは
$${△CHE=}\frac{1}{4}{t^2}$$
①と②を連立すると(加減法)
$$\frac{1}{4}{=}\frac{35}{2}$$
となりまして、求められました。
まとめ
この問題は難問ではありますが「与えられた面積と、求めたい三角形の面積を式にしやすいこと」と「同じ面積を知るための合同な図形が、先に入っている記号から分かること」の2点により、難問ではあっても丁寧に行えば比較的普通の考え方で解答に至れるように思います。補助線として引いたのは△DFGの高さだけで、これも基本的な考え方ですから、ムリな補助線ではないでしょう。
ということで、基本を使うトレーニングをしっかり積めば、確実に解けるようになる問題と思います。2024年6月の北辰中3第2回の数学は100点が狙えたテストだったのではないかと思います。
一応「お前は時間内に100点採れるのか!」とツッコまれた時のために、今回の北辰の問題を私が解いたとき、30分ほどで100点でした。ただ、これは頭が良いというより、単に年の功というやつです。30年ほど前、中1のとき受けた北辰テストでは私の数学の偏差値は48くらいでした。勉強をするようになった中3の後半でも62くらいでしたから、特に頭が良いというわけではないと思います。大体、小6になっても、かけ算の筆算が十分にできないくらいの賢さでしたから。それでも基本に忠実に長年続ければ、このくらいはできるようになるということだと思います。
もし、小3くらいでかけ算の筆算がそれなりにできるような人であれば、基本を使えるように勉強をすれば、もっと短い時間でこのくらいはできるようになるのではないかと思います。そして、ぜひ将来、基本を使える大人になって活躍してほしいといつも願っています。私は、このような「基本を使えるようにする学習」を広く教えていけることを日々夢見ています。
とはいえ、100点で偏差値80です。夢の偏差値ですね。

