2024年6月実施の中学3年第2回北辰テスト数学。目標偏差値ごとに、解きたい問題、次の目標となる問題などの目安を考えてみました。
それぞれの問題をできるようにするには、どんなことを目標に勉強をすればいいのでしょうか?
偏差値74へのチャレンジ 第2問(4)
第2問(4)は体積を求める問題です。この第2問の(4)あたりには、難しい図形問題が配置されていることが多いです。
今回も偏差値74へのチャレンジ問題と感じます。ただ、難問というよりは、今回の全問題の中で2番目に攻略が難しい問題と感じるためです。
ただ、第2問(3)は正攻法で解こうとすると、この第2問(4)より難しいですが、ちょっとズルい(しかし正統的な)方法で解こうとすると易しい問題になります。
また、データ的にはこの第2問(4)より第3問(2)の方が正答率が低いですが、第3問(2)は関数のため、練習の仕方をしっかりすれば、比較的簡単に解法にたどり着けます。
これらのため、この第2問(4)が全体で2番目に攻略が難しいと考えています。
第2問(4)のための知識の確認
第2問(4)を解くために必要な知識は次のようなものです。
・三角錐の体積の求め方
これだけです。
第2問(4)を解きます
問題文を読みながら、図に情報を書き込んでいくと、次のように書き込まれます。
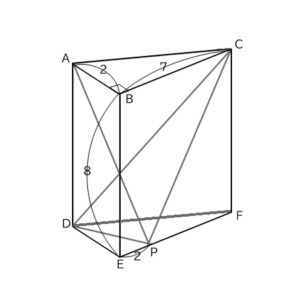
この図形で、三角錐ACDPの体積を求めよという問題です。
三角錐の体積を求めます。求め方は
$${底面積×高さ×}\frac{1}{3}$$
でした。
ですから「底面はどこで、高さがどこか」をまずは決めます。
底面の候補は△ADC、△DPC、△APC、△DPAの4つの面が候補になります。三角錐ですから、これ以外に面はありません。
このうち、第一候補は△ADCでしょう。というのも、この三角形だけがもとの三角柱の面上にあるからです。ほかの三角形は元の三角柱の面上にないので、面積を求めようと思ってもちょっと厄介そうなので、後回しにします。
さて、△ADCを底面とすると決めましたので、高さはPから面ADCに引いた垂線となります。これを書き込んでおきます。
ついでに、底面となる△ADCと高さとなる線分のある面DEFも抜き出しておきます。
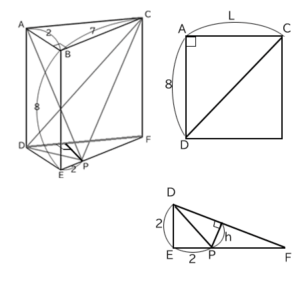
ここで、底面となる△ADCの面積を求めるとき、ACの長さが分からないので、文字Lで置いておきます。
同じように、高さとなる点PからDFに引いた垂線の長さも分からないので、hと文字で置いておきます。
この段階で、求める三角錐の体積は次のような式になりました。
$${体積=L×8×}\frac{1}{2}{×h×}\frac{1}{3}$$
さて、ここまで来ましたが、Lとhが解決していないのでどうにもなりません。そこで、Lと同じ長さが他の辺にもあるので、これを書き入れてみます。
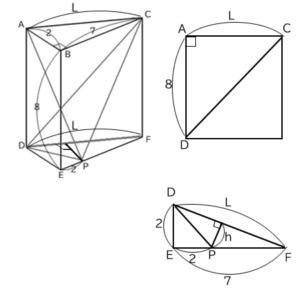
すると、右下の△DEFにLとhの両方が書き込まれていますので、この図を使って進めていきましょう。
そして、次が最も難しところです。そして、考えて的に妙な流れです。
△DFPの面積を使いましょう。なぜか?そうすると、L×hが作れそうだからです。
$${△DFP=△DEF-△DEP}$$
$${7×2×}\frac{1}{2}{-2×2×}\frac{1}{2}$$
$${=5}$$
また、
$${△DFP=L×h×}\frac{1}{2}$$
これより
$${L×h×}\frac{1}{2}{=5}$$
$${L×h=10}$$
これで、三角錐の体積の式も解決です
$${体積=L×8×}\frac{1}{2}{×h×}\frac{1}{3}$$
$${=4×L×h×}\frac{1}{3}$$
$${=4×10×}\frac{1}{3}$$
$${=}\frac{40}{3}$$
これで求められました。
まとめ
この問題では、図形問題でも色々と試行錯誤する前にできるだけ普通に体積を求めようとすべきでしょう。このとき、数学の最大の武器の1つ「文字で置く」は使った方がいいと思います。文字で置くことで、とりあえず式にすることができます。式にしてから「さて、その文字をどうしようか?」と考え始めます。
文字で置いて式にして、式を整理することで、これまで見ていた視点と別の視点を見えやすくしてくれる感じです。これが数学が強力に私たちの思考をサポートするということの1つですし、中学生からの解き方の基本となります。
この問題では、三角錐の体積の式を作ったところで「L×h」の値が必要になりました。Lの値でも、hの値でもいいのですが、L×hでもいいのです。
そして、L×hの値を探すことに成功して、解くことができました。
この問題で難しいところは次の2つの部分でしょう。
・三角錐の高さがどこか?
・L、h、またはL×hのどれかの値を知ることと、そのために、△DPFを使うこと。
これらは確かに難しいです。だから偏差値74へのチャレンジ問題なのですが、ムリなレベルではないと思います。

