2024年6月実施の中学3年第2回北辰テスト数学。目標偏差値ごとに、解きたい問題、次の目標となる問題などの目安を考えてみました。
それぞれの問題をできるようにするには、どんなことを目標に勉強をすればいいのでしょうか?
偏差値65超えへのチャレンジ 第1問(9)
第1問(9)は図形の折り返しについての問題です。
これが偏差値65超えへのチャレンジ問題である理由は2つ。
1つ目は単に折り返し問題を苦手にしている中学生が多いこと。
2つ目は図形問題であること。
折り返し問題は苦手だという中学生の意見は良く聞きます。なのに、折り返しの問題は北辰テストでも公立高校入試でも、そこそこ出るタイプの問題です。
次に、図形問題というのはどちらかと言えば数学より算数に近い問題です。数学は、いろいろなことを数式で表すことにより、複雑なことを簡単に扱えるようにします。この特徴により、私たち人類は複雑なことでも扱えるようになり現代技術を作って来ました。これと同時に、この特徴により、ちょっとだけ複雑なことを簡単に扱えるようになります。
簡単に扱えるようになるというのは、私たちが頭を使って考える手助けを数式がしてくれるということです。そのため、過去においては天才と言われるような能力の持ち主しか扱えなかった事柄を、数式を使うことにより普通の能力の人でも扱えるようになりました。
入試問題も同じです。数式を使って表すことができれば、あれこれと考えることは軽減されます。「こんなのだれが思いつくんだよ!」というような、ひらめきの必要も少なくなります。
これが数学の持つ力であり、凡人にとっての光明です。
けれども。図形問題は、数式で表して扱えるようになるのは、高校数学の関数やベクトルを待たなければなりません。数式で表すことができないという部分において、算数に近いと思います。
数式で表せることが少ないために、高校受験では、図形問題はまだ、地頭に頼らねばならない部分が多少なりともあります。このため、解けるようになるのが難しいとも言えます。(これはつまり、関数など数式が使える問題は、地頭に頼る必要は少なくて済み、普通の頭の人でも難なく解けるということです。また、高校、大学と進むにつれて、普通の人でも扱える部分が多くなっていくということです。少なくとも純粋な数学以外の、数学を利用して何かをするような数理科学や物理学では。)
第1問(9)のための知識の確認
第1問(9)を解くために必要な知識は次のようなものです。
・長方形の特徴
・平行線の錯角
・折り返したときの、元の部分と同じ長さと角度になる部分
第1問(9)を解きます
問題文を読みながら、図に情報を書き込んでいきます。
まず「四角形ABCDが長方形」ということですから、次のように書き込まれます。
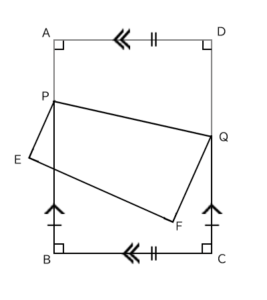
次に「線分PQで折り返した」ということですから、さらに次のように書き込まれます。直角が4つと、2組の対辺が平行で同じ長さであることが書き込まれます。
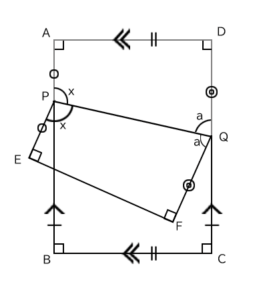
角APQは問題文でxと文字で与えられています。
角DQPを文字aとしました。
折り返したので、角APQ=角QPE、角DQP=角FQPです。その他、直角と同じ長さの線分が書き入れてあります。
次に「角CQF=30度」と問題文で指示されます。
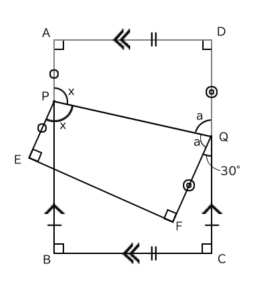
これで、問題文で与えられたことが大体書き入れられました。この段階では、まだどれを使うか、どう解くか分かりませんから、とりあえず色々と書き込んであります。この状態から、xの大きさを求めます。
ここから「どうしようか?」と考えますが、求めるのは角の大きさですから、まずは角に着目します。
ここでキーワードは「長方形」と「折り返し」です。折り返しについては、同じ大きさの角は書き込み済みです。
「長方形」については、直角は書き込んであります。
ただ長方形ということで書き込んだ「平行」という性質も「錯角」と「同位角」が等しいという性質がありしたから、これを探します。
すると、次のような形を見つけられるでしょう。ここがこの問題で一番難しいところです。
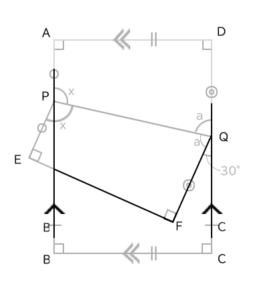
このように、2本の平行線が折れ曲がった線でつながっている形、見覚えがあるでしょうか?
中2で錯角や同位角を学んだときに、よく出てきた形です。この問題は、できる人も多いと思います。
折れ曲がりに平行な線を入れて、錯角を使っていきました。
同じようにやっていくと、次のようになります。
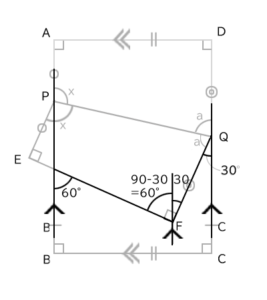
すると次に、対頂角が使えて、求めたい角度xに近づいていけます。
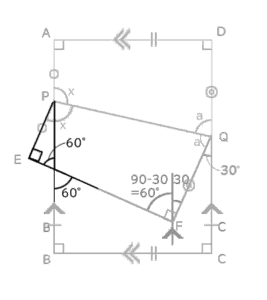
ここで、三角形の内角の和が180°であることから、角EPB=30°と分かります。xに近づいてきました。
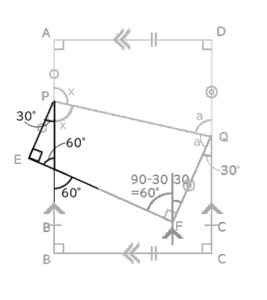
今、分かった30°はxに近い角ですから、この周辺を見てみると、角QPB=x-30と分かります。
そして、次のようにしてxについての式ができます。
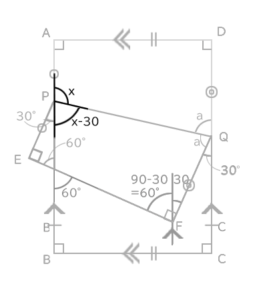
x+(x-30)=180
これより、 x= 105° と求められます。
まとめ
この問題では、錯角を使った形が「見えるか?」が解けるか解けないかに関わっていました。
前回扱った第1問(7)では「定義、読み取り、丁寧な扱い」という視点が大切でした。これは数式で表すときでも大切なことですから、数学力の基礎と思います。
今回の第1問(9)は算数に近い問題ですから、このような数学力の基礎が特に必要というわけではありません。トレーニングしづらい問題です。
このような問題は「慣れ」の必要性が大きいように思いますから、丁寧な練習より、多くの類題での練習が必要になると思います。普通の勉強法で学習を進めていても、量で解けるようになる問題とも思います。

