2024年9月1日実施の中学3年第4回北辰テスト数学。目標偏差値ごとに、解きたい問題、次の目標となる問題などの目安を考えてみました。
それぞれの問題をできるようにするには、どんなことを目標に勉強をすればいいのでしょうか?
偏差値70へのチャレンジ 第4問(3)
第4問(3)は北辰テストの最後の問題ですが、ほぼ毎回、難問で正答率もかなり低いです。
とはいえ、難問でも、本当にムリな問題から、丁寧に進めれば解くのは比較的ムリではない問題まであります。
2024年9月の中3第4回は、比較的簡単に解けるレベルでした。進め方を軽く触れてみます。
第4問(3)のための知識の確認
第4問(3)を解くために必要な知識は次のようなものです。
・三角形の面積の求め方
・分数が比を表すこと
第4問(3)を解きます
(1)の合同と、(3)の問題文で与えられた条件を図に書き込んでいくと、まずは次のように書き込まれます。
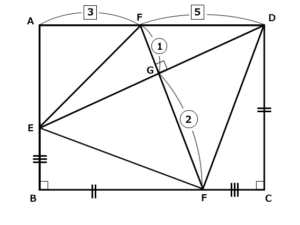
また、問題文には
$${△EFDの面積が四角形ABCDの面積の}\frac{5}{12}{倍}$$
という条件もあります。
これらから EB:BF の比を求める問題です。
さて、通常であれば与えらえた辺の比 FG:GH=2:1 , AH:HD=3:5 から面積の比などを使って解き進めます。けれども、まだ問題文で与えれた条件と、求める辺の比がどう使がるかがいまいち分かりません。おそらく面積を使っていくのだろうとは思いますが、まだカンのようなものでしかありません。
△EFDと四角形ABCDの面積の条件はまだ図にも入れていません。また、この部分は式にできますが、式にもしていません。この2つを行っていくことで、もしかしたら「どのような形で情報をまとめていけばいいのか」が分かるかもしれません。まずはこれがやってみます。
図に入れるのは、例えば次のような感じです。
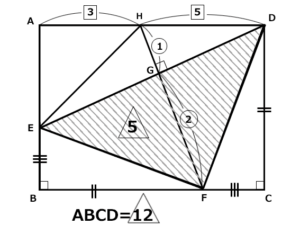
△EFDの面積が5と入ります。比の値ですから、面積が5というわけではありませんが、ここから先は面積を5とおいて進めていきます。
ここでEDとFGが垂直で、FGに比の値が入っていることから、EDを底辺、FGを高さと見ていくのが、最初の方針と考えられます。また、このようにみると△HEDを底辺がED、高さをHGするのが見やすく、△HEDの面積へとつながります。
△HEDと△EFDは底辺EDが同じで、高さがHG:GF=1:2ですから、面積も1:2です。
$${△HED=}\frac{1}{2}{×△EFD=}\frac{5}{2}$$
△HEDと△AEHの面積を考えると、△HEDは底辺AH、高さAE。△AEHは底辺HD、高さAEとすると、高さが同じです。面積はAH:HD=3:5 です。
$${△AEH=}\frac{3}{5}{×△HED=}\frac{3}{2}$$
面積が求められていないのは△EBFと△FCDですが、これは合同です。
$${△EBF=(四角形ABCD-△DEF-△HED-△AEH)×}\frac{1}{2}$$
$${=}\frac{3}{2}$$
さて、ここまでやってきましたが、BEとBFの辺の長さとつながりません。
BEとBFの長さを文字で置き式にしていきます。
$${EB=a, BF=b}$$
と文字で置きます。(1)で証明した合同がありますから、FC,DCも文字が入ります。
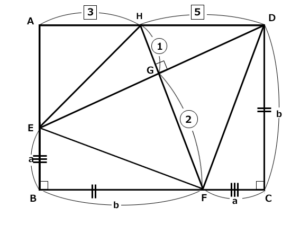
$${四角形ABCD=(a+b)×b=12}$$
$${△EBF=ab×}\frac{1}{2}{=}\frac{3}{2}$$
これより
$${ab=3}$$
これを代入して
$${b=3}$$
$${a=1}$$
これより、EB:BF=1:3と分かりました。
まとめ
この問題は難問ではありますが「三角形の面積で、底辺と高さに注目する」という小学生から使っている基本的なことで面積が分かっていきます。
けれども、辺と面積のがつながりません。
これは、辺を文字で置けばすぐに式にでき、この式から答えが出ます。
ということで、基本を使うトレーニングをしっかり積めば、確実に解けるようになる問題と思います。2024年9月の北辰中3第4回では、この問題は偏差値70以上を狙うにはチャレンジすべき問題でしょう。

