2023年6月実施の、中学3年第2回北辰テスト。
比較的シンプルな問題でありながら、正答率が低い問題が2題あります。
第2問(4) と 第3問(2) です。
第2問(4)の正答率
全体 4.5%
偏差値70以上 50.6%
偏差値65以上 20.6%
第3問(2)の正答率
全体 2.5%
偏差値70以上 23.1%
偏差値65以上 8.7%
これらの問題を解くには、それほど高い実力が必要なわけではないと思います。第2問(4)についてみてみます。
正答率の低い問題、本当に難しい?
第2問(4)で使う基礎知識は次の4つです。
・円錐の展開図
・おうぎ形の面積の式
・おうぎ形の弧の長さの式
・円錐の展開図で、側面の弧の長さと、底面の円周が等しいこと
この2つは偏差値55くらいから知っている人が多いものです。
第2問(4)
第2問(4)を解き進めます。
解き方は「問題に従うこと」だけです。
問題に従うというのは以下の3点です。
・問題文を読みながら、図を描いくこと。
・図に長さや角度を書き入れること
・面積等が指定されたら、式で書いておくこと。
(このとき、ここで作った式が、問題を解くために必要かどうかはまだ分からなくて大丈夫です。問題の指定する条件がどうなっているかを知るための作業ですから、この段階では使うか分からなくても書いておきます。コレ、とても重要なことです。もちろん、メンドウな式なら、保留にして書かずにすすむこともあります。また、値が分からないときは、文字で置きます。)
進めます。
問題文を読んでいくと
「母線ABの長さ9cm、底面の円Oの半径が5cmの円錐」とすぐ出てきますから、これを図に書き入れます。
次に、点Bと点Cが指定されます。この2点は図に書いてありますので、確認します。
そして「側面のうち」と、側面を見るように指定されますので、ここで展開図を書きます。
弧BC(短いほう)で囲まれた側面の面積を与えられますので、図に書き込み、式にします。
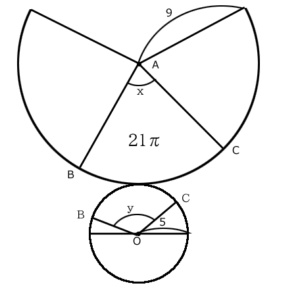
側面のおうぎ形の中心角が分からないと、おうぎ形の面積を式にできないので、xとします。
$${9^{2}}\times\pi\times\frac{x}{360}{=21}\pi$$
とりあえず、この式はxの方程式になっていて解けるので、解いてxの値を求めておきます。
$${x=}\frac{7\times{40}}{3}$$
ちょっとメンドウな計算になりましたので、7×40は計算せずに、このまま書いています。
とりあえず、先に進みます。すると「角BOCの大きさを求めよ」とあります。
いま、側面を扱っていましたが、求めるのは底面です。
側面と底面を結びつけるのは、側面の弧の長さと底面の円周です。
側面の弧の長さと、底面の円周が等しくないと、組み立てても円錐にならなくなります。
これと同じく、側面の弧BCと底面の弧BCが等しくなければなりません。
これを式にすします。角BOCをyとして、式を作ります。
これが、この問題で一番難しいところです。このとき、さっき求めたxの値を最初から使うのはやめて、式で書いておきます。使ってもいいのですが、分子に分数が入ると複雑に見えてしまうので、やめておきます。
$${9\times2\times\pi\times\frac{x}{360}=5\times2\times\pi\times\frac{y}{360}}$$
この式を整理すると
$${y=\frac{9x}{5}}$$
これにさっき求めたxを代入して
$${y=\frac{9}{5}\times{\frac{7\times{40}}{3}}{=168}}$$
これで角終わりです。
途中が少し長いですから、問題文を最後まで読んでから解こうと思うと、混乱してしまって難しいと感じるかもしれません。
「どうなっているか」が分からないのに「どう解こうか?」と考えれば難しいのは道理です。「どうなっているか」を頭の中だけで把握しようとする習慣が、問題を難しく感じさせると言ってもいいのかもしれません。だから、よみながら「どうなっているか」を書き表していきます。
このとき、側面の弧と底面の弧の比と、それぞれの中心角の比などの知識は特に必要ありません。
問題文を読みながら、その順に従って図を描き、式を作っていきます。ただ、難しのは「側面の弧BCと底面の弧BCの長さが等しい」という式です。同じ弧BCですから、それほど難しくないと感じる人もいるでしょうが、こおの式を作っておけるかがカギです。
このように条件を把握しながら進めることは、勉強ができる人からすれば当たり前に思えることかもしれませんが、普通の人にはそれができないことが多いのです。けれども、この進め方を学べば、普通の頭の人でも偏差値70は超えられます。
条件を把握しながら進めることが当たり前と思える人も、体系的にこの視点を身に着けられたら、もっと明確になりますから、もっとできるようになるでしょう。

