2023年6月実施の、中学3年第2回北辰テスト。
やや難しいですが、一次関数「傾き」の応用。この問題より難易度の高い問題は第4問(3)くらいですから、おそらく、この問題を解けたら偏差値78いくかも!
第2問(5-2)の正答率
全体 1.7%
偏差値70以上 27.5%
偏差値65以上 7.8%
これらの問題を解くには、傾きの基礎知識が使えそうです。
傾きの基礎知識
一次関数の傾きの基礎知識
式では
$${傾き=}\frac{yの増加量}{xの増加量}$$
グラフでは
$${傾き=}\frac{たての変化量}{よこの変化量}$$
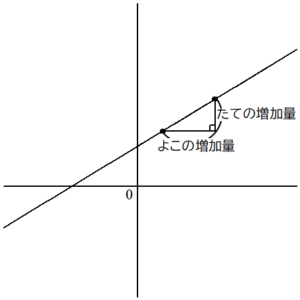
比較的多くの人が知っているであろうこの知識で解けます。
第2問(5-2)
第2問(5-2)を解き進めます。
縦の長さが a、横の長さがbの長方形に長さ1ずつの正方形(格子)が入っている図形で、左上から右下の「対角線と縦横の線との交点の個数を求めよ」という問題です。
(5-2)では a=20、b=35 (たて20、よこ35)の長方形についてです。
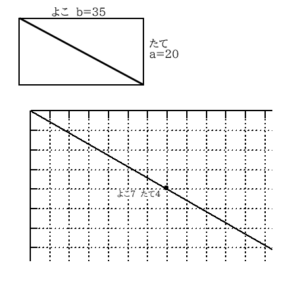
この対角線、傾きに似ています。ですから、傾きのように考えると
$${傾き=}\frac{-20}{35}$$
です。
約分すると
$${傾き=}\frac{-4}{7}$$
この式は「よこに7、たてに-4の上図で格子の交点と交わる」ことを表すと読み取ることができます。そして、この間には、格子の交点を通らないことも、図と合わせれば読み取れるでしょう。対角線の左上の始まりから、(よこ7 たて4)の点までには、縦の線と6回、横の線と3回交わっています。負の数はわかりずらいので(よこ7、たて4)と表しています。
実際に解く際には、よこ10たて8くらいの図を描いて確かめると分かりやすいと思います。
ここまでで縦横の線と交わった点は、(よこ7 たて4)の点を含めて
$${6+3+1=10}$$
より10個です。
これを繰り返します。
(よこ7、たて4)から(よこ14、たて8)まででさらに10こ、ここから
(よこ14、たて8)から(よこ21、たて12)までででさらに10こ
(よこ21、たて12)から(よこ28、たて16)までででさらに10こ
(よこ21、たて12)から(よこ35、たて20)までででさらに10こ。ただし、これで長方形の右下にたどり着いたので、この点を含めてはいけないため、9こ
こうして
$${10}\times{4}{+9}=49$$
49個が求める交点の数となります。
どうやって思いつく?
この方法はどうやったら思いつけるか?と考えてみると
「単に、傾きのグラフでの絵と似ているから」
と思います。「似ている」は大切です。
ただし傾きを学ぶときに「傾きがグラフで何を表すのか?」とか「傾きから読み取れること」を練習しているかどうかによるかもしれません。基礎の学習のしかたで、結構差が開きますので、基礎学習は侮れません。
以上、正答率1.7%の問題ですが、解くための知識は比較的簡単なものでした。

