2023年6月実施の、中学3年第2回北辰テスト。
全体の正答率が10%未満の問題が5問あります。
正答率の低い順に
第4問(3) 0.0% 配点5点
第2問(2) 1.7% 配点5点
第3問(2) 2.5% 配点6点
第2問(4) 4.5% 配点4点
第1問(11-2) 6.7% 配点3点
このうち正答率の低い2問ができなくて、それ以外ができた場合には90点で、偏差値76.6となります。夢のような偏差値!
でも、第3問(2)実は難しくありません。
第3問(2)の正答率
全体 2.5%
偏差値70以上 23.1%
偏差値70から65 8.7%
偏差値65から60 4.7%
こんなに正答率が低いのに、難しくないとはどういうこと?
第3問(2)を解くために必要な基礎知識
第3問(2)を解くために必要な基礎知識は次の4つです。
・1次関数で、直線の通る点は式に代入。
・1次関数で、2直線が平行なとき、傾きが等しい
・傾きのグラフでのみかた
$${傾き=}\frac{たての変化量}{よこの変化量}$$
・平行四辺形の性質「1組の対辺が平行で長さが等しい」
これらは偏差値60以上の受験生であれば、ほとんどの人は知っている内容です。そしてこれらが適切に使えれば、考えなくても解けます。
第3問(2)を解く
数学でまず大切なのは「問題を読んでから、どう解こうか考える」のではなく、「問題を読みながら、どうなっているかを把握していくこと」です。
実は「あまり解こうとしない方がうまくいく」という場合が多いと感じます。
問題文を読みながら、どうなっているかを把握していきます。
まず、スタートの段階で
点Aの座標と直線lの式が与えられます。
$${点A (6,4)}$$
$${直線l:y=-2x+b}$$
また、線分OAと点Pも与えられます。
グラフの方が見やすいので、グラフに書き入れておきます。
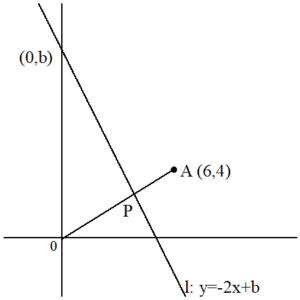
直線lの切片が +b となっていますから、これもグラフに座標で書き入れておきます。
次に(2)を読み進めながら、グラフに書き入れていきます。
「まず点Aを通り、直線lに平行な直線をひく」とありますから、式とグラフで書いておきます。
式 では、lと並行なので傾きは-2、切片は分からないので文字kで置いておきます。
$${y=-2x+k}$$
これが、点A(6,4)を通るので、代入してみます。
$${4=-2×6+k}$$
解いてkがそれほど手間なくを求められそうなので、求めておきます。
$${k=16}$$
これをグラフに書き入れると次のようになります。
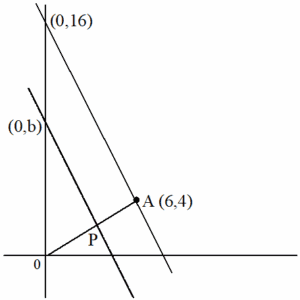
次に、問題文では「このlと平行な直線とx軸との交点をBとする」とありますから、点Bを式にして、グラフに書き込みます。
x軸との交点では、y=0ですから
$${0=-2x+16}$$
これも、それほど苦労せずに解けますので、解いてしまいます。
$${x=8}$$
点Bの座標は(8,0)となります。
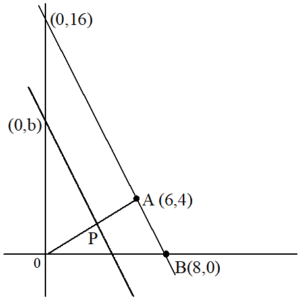
次に問題文では「直線lとy軸との交点をQとする」と「四角形AQPBが平行四辺形となる」と言われます。ここで点Pも必要になるので、点Pを求めます。
けれども、そもそも点PはOAとlの交点ですOAの式が必要になります。
傾きを求めると
$${OAの傾き=}\frac{4}{6}$$
$${=}\frac{2}{3}$$
これより、OAの式は
$${y=}\frac{2}{3}{x}$$
点Pを求めるので、直線lと連立(代入法)します。
$${-2x+b=}\frac{2}{3}{x}$$
この式はbが入っているので、整理するのはメンドウですから、このままとっておきます。(試験中では、問題用紙に書いておくだけ。)
それから、これまでのグラフでは、平行四辺形に見えないので、ちょっと書き直します。
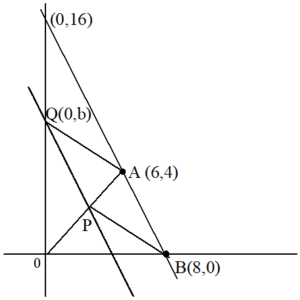
さて、Pを求めるのは保留したので「平行四辺形ならどうなっていればいいか」をグラフに書き込みます。
AB//QPなら、ABの傾きとQPの傾きが同じということです。このとき、グラフには直角三角形を書き入れます。
ABから、直角三角形の縦と横が分かります。
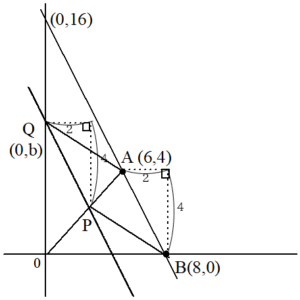
この直角三角形は約分していません。約分ないで横と縦が同じなら、合同になりますから、平行で長さが等しいことになります。
すると、ここから点Pのx座標が 2 と分かってしまいました。
y座標は b-4 です。
これがOA上にないといけないので、OAの式に代入しておきます。
$${b-4=}\frac{2}{3}{×2}$$
おや、bが求めれそうです。解いてしまいましょう。
$${b=}\frac{16}{3}$$
さて、問題は最後「bの値を求めなさい」となります。
ですから、これで終わりです。
平行四辺形になるために、傾きで平行を考えます。そのため、グラフに直角三角形を書き入れました。この問題で難しいのは、この部分だけでしょうか。
他は、問題文に従って、点の座標を代入すること、x軸との交点でy=0を代入すること、という基本的な扱いだけでした。
結局、OAと直線lの連立した式は使いませんでした。結果として使わなかっただけで、あの段階では使うか使わないかは分かりません。だから、式を書いておいておきました。
これが正答率2.5%の問題です。
妙に思うこと
問題3(2)はこのように、基本的なことを行っていけば、それほど考えなくても解けてしまいます。
妙なのは、この問題の正答率が全体で2.5%なのに対して、もっと問題文が長くて少し考えないと解けない問題2(5-1)の正答率が15.6%ということです。
正答率を比べると
問題2(5-1) : 問題3(2)
全体 15.6% : 2.5%
偏差値70以上 90.0% : 23.1%
70から65 67.7% : 8.7%
65から60 35.7% : 4.7%
問題文の長さは問題2(5)の方が圧倒的に長いです。
また、問題2(5-1)は問題文で説明されたことを式にするということでは、問題3(2)と変わりませんが、書いてあることをそのまま式にできないため、ちょっと考えなければなりません。
問題2(5-1)の方が、やや複雑で思考力が必要と考えられます。なのに、こちらの方が正答率が高くなっています。
これは、いわゆる「論理的思考力」に関しては、学習の成果が出ているのかと思います。
論理的思考力というのは、私たちの脳をつかってあれこれと考えることです。言葉と脳が考えの主軸となると思います。
これに対して、問題3(2)は数学の基本的扱いによって解かれます。論理的思考力は、それほど必要ありません。
そもそも、数学は私たちの脳では扱え切れない複雑ななことを扱える道具(パソコンを使った数理科学の技術も含めれば、もしかしたら人類の持つ唯一の道具)と私は考えています。
人間の頭で考えて、扱えるのは結構単純な問題までです。多数のもの(3つ以上)の要素が互いに関連しあう事柄となると、想像することすら難しくなります。
例えば、磁石2つを机の上で指で近づけておいて、それから指を離したらどうなるかは想像できるかもしれません。これが、磁石3つになると想像するのも難しくなります。でもまだたった3つの磁石です。世の中ので起こる現象は、これ以上に多数が関わり、相互の関係も複雑です。
そのため、これ以上のことを考えるには数学を使った補助がどうしても必要になります。
(もちろん、相手が人間であれば、人間の論理以外の思考(経験による直感や感覚)が効力を発揮して、数学を使うよりうまく扱えるでしょうが。)
さて、現代では2つの要素のような事柄ではなく、3つ以上の要素が絡み合う事柄の方が多いでしょう。このような時代において、数学を論理的思考力のために学ぶだけではなく、数学を使って様々な事柄を扱う道具として学ぶ必要の方が大きいのではないかと思います。(これは「解き方」を学ぶのではありません。)
そして、このテストの正答率の比較から、論理的思考力が学習はそれなりにうまくいっているようにも思います。パズルのような問題をやったり、数学は国語力が大切だとして文章理解力を付けるような学習が行われていますから、これらは効果があるのだと思います。
一方で、基本的な扱いを行っていくだけで解ける第3問(2)すら低い正答率になることから、、数学を扱う力の学習は、あまりうまくいっていないように感じます。
数学は私たちの頭では扱え切れない複雑な問題を扱う道具です。これは同時に、数学を適切に使えば、入試くらいの問題であればあまり頭を使わずに比較的楽に扱えるということです。
自頭がなくても、数学を使えば、余裕で補えます。応用問題が解けなくて不安な人、大丈夫です、できるようになります。

